Before describing StratAge, I hope to motivate its design by reflecting on the humble stratigrapher.
Stratigraphy
The job of the stratigrapher is to discretize a pile of sediments into units (“beds”). How we decide to do so depends on the scale of the questions we are trying to answer, which can range from tectonostratigraphy on packages that are kilometers thick to investigation of mass extinction horizons over a handful of meters.

To lump or to split...stratified diamictite, including climbing ripples on a glacial dropstone in the Ghaub Formation at Fransfontein Ridge in Namibia.
Regardless of spatial scale, the stratigrapher must decide how to “lump” and “split,” a task that is facilitated by the natural occurrence of bedding contacts that separate intervals of deposition. Inexperienced stratigraphers often tend to excessively split. This behavior results from the fact that bedding contacts occur at various scales in stratigraphy, and the closer you look, the more you find. In this sense, stratigraphy exhibits fractal-like self-similarity,1 which is the spatial manifestation of the Sadler Effect.2
The Sadler Effect is the phenomenon that apparent accumulation rates decrease as a power law with averaging timescale. A single ripple can accumulate 1-10 cm in minutes and hours, but this rate extrapolated to geologic timescales would impossibly imply thousands of kilometers of accumulation. The apparent slowing results from the incorporation of missing time — hiatus. More precisely, the power law distribution of hiatus duration causes the power law relationship in the Sadler Effect.3 Hiatus, and the vast majority of stratigraphic time, exists at bedding contacts.
With this perspective, the job of the stratigrapher attains some clarity: we split sufficiently to isolate units accumulated over similar timescales. Sadler2 demonstrated that over similar timescales, within an order of magnitude, sedimentation rates exhibit a log-normal distribution. The perfect stratigrapher lumps such that no bed contains a contact with a hiatus longer than any hiatuses separating beds. If we do a good job, then the contacts we identify contain information about where time is missing.
Age Modeling
Existing stratigraphic age-depth modeling frameworks (Bchron, Bacon, Chron.jl) all perform age modeling directly in absolute time using geochronologic constraints provided by the user. Bacon and Chron.jl furthermore permit the user to specify hiatus occurrence at specific heights. The preceding dicussion, however, has hopefully motivated that nearly all stratigraphic time occurs in the form of hiatus at bedding contacts, which occur throughout a stratigraphic section.
If we trust the stratigrapher’s work, then we can leverage a stratigraphic section to explicitly allocate time into beds (as sedimentation rates) and contacts between beds (as hiatuses). This approach directly links the distribution of stratigraphic time with the structure of stratigraphy. Importantly, this approach also allows the specification of prior distributions directly over empirically constrained, physical quantities, like sedimentation rates and hiatus durations. In contrast, existing age modeling approaches model more abstract monotonic processes, whose priors are over parameters that are not directly related to stratigraphy, reducing physical interpretability.
By modeling stratigraphic time as sedimentation rates and hiatus durations, StratAge utilizes a completely new approach that operates first in floating time. The details of this new approach are described with a synthetic toy example in the package documentation (as well as in a forthcoming manuscript). Ultimately, the floating age models can be anchored in absolute time to generate a Bayesian age-depth model.
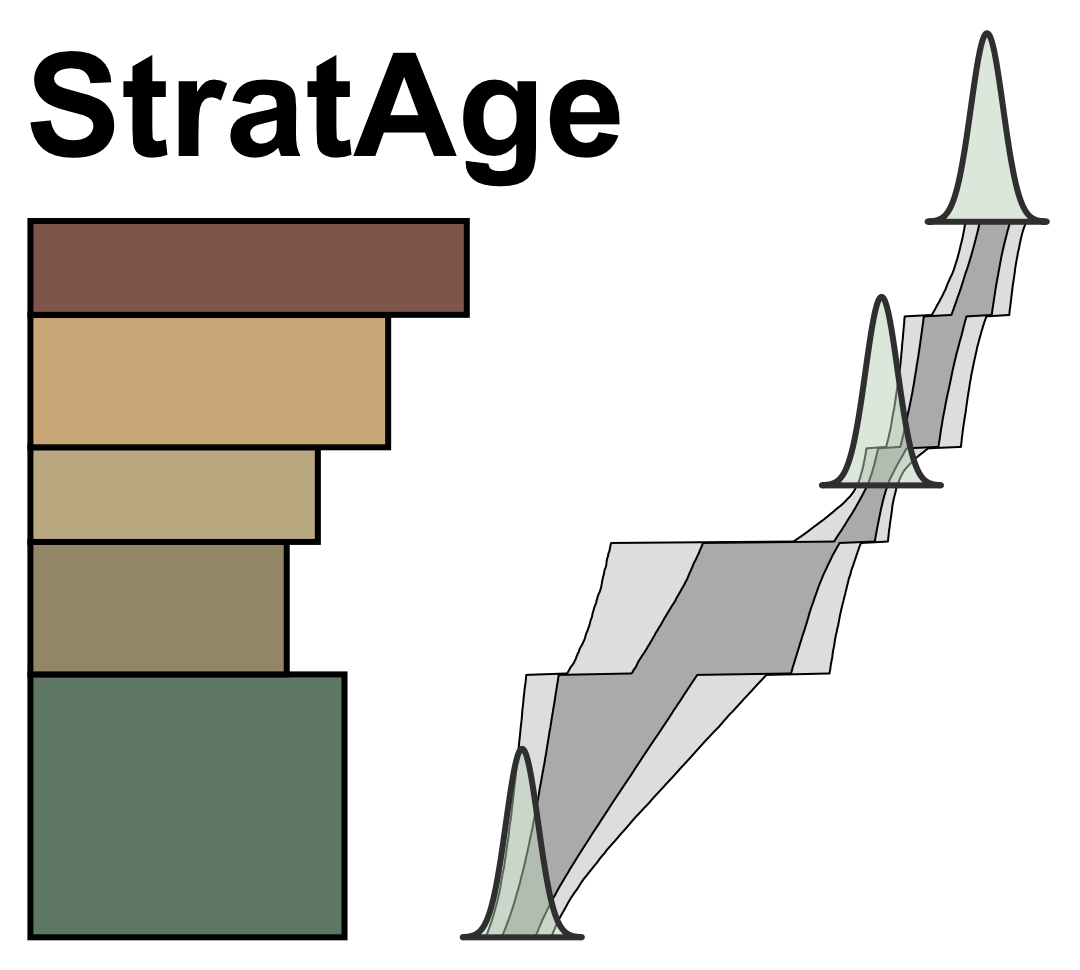
StratAge logo, showing a 'jumpy' posterior age model consistent with the Devil's staircase behavior of stratigraphy.
An example of such an age model is shown in the package logo above, where jumpiness in the posterior ages reflects the posterior distribution of hiatus at bedding contacts. This structure more accurately reflects the physical distribution of time in stratigraphy, which we know operates as a “Devil’s Staircase.” This modeling approach also generates posterior distributions over bed sedimentation rates and bedding contact hiatus durations. These outputs can be used to infer stratigraphic completeness and compensational sedimentation from a single stratigraphic section (presented in a forthcoming manuscript).
StratAge is available as a python package on PyPI, which can be installed as
pip install stratage
Plotnick, R. E. A Fractal Model for the Distribution of Stratigraphic Hiatuses. The Journal of Geology 94, 885–890 (1986). doi:10.1086/629094 ↩︎
Sadler, P. M. Sediment Accumulation Rates and the Completeness of Stratigraphic Sections. The Journal of Geology 89, 569–584 (1981). doi:10.1086/628623 ↩︎ ↩︎
Schumer, R. & Jerolmack, D. J. Real and apparent changes in sediment deposition rates through time. J. Geophys. Res. 114, F00A06 (2009). doi:10.1029/2009JF001266 ↩︎